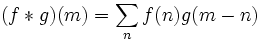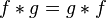반응형
합성곱(合成-, 영어: convolution 컨벌루션[*])은 하나의 함수와 또 다른 함수를 반전 이동한 값을 곱한 다음, 구간에 대해 적분하여 새로운 함수를 구하는 수학 연산자이다.
정의[편집]
두 개의 함수  와
와  가 있을 때, 두 함수의 합성곱을 수학 기호로는
가 있을 때, 두 함수의 합성곱을 수학 기호로는 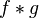 와 같이 표시한다.
와 같이 표시한다.
합성곱 연산은 두 함수 f, g 가운데 하나의 함수를 반전(reverse), 전이(shift)시킨 다음, 다른 하나의 함수와 곱한 결과를 적분하는 것을 의미한다. 이를 수학 기호로 표시하면 다음과 같다.
또한 g 함수 대신에 f 함수를 반전, 천이 시키는 경우 다음과 같이 표시할 수도 있다. 이 두 연산은 형태는 다르지만 같은 결과값을 갖는다.
위의 적분에서 적분 구간은 함수 f와 g가 정의된 범위에 따라서 달라진다.
또한 두 확률 변수 X와 Y가 있을 때 각각의 확률 밀도 함수를 f와 g라고 하면, X+Y의 확률 밀도 함수는 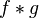 로 표시할 수 있다.
로 표시할 수 있다.
이산 합성곱[편집]
이산 함수의 경우, 합성곱을 다음과 같이 정의 한다.
두개의 다항식을 곱한 결과식의 계수는 원래 다항식의 계수들의 합성곱으로 나타낼 수 있다.
특성[편집]
합성곱은 다음과 같은 성질들을 만족시킨다.
교환 법칙[편집]
결합 법칙[편집]
분배 법칙[편집]
스칼라 곱의 결합 법칙[편집]
실수 혹은 복소수 값 a에 대해서
미분 법칙[편집]
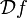 는 함수 f의 미분 값을 나타낸다. 또는 이산 함수에서 미분 연산자
는 함수 f의 미분 값을 나타낸다. 또는 이산 함수에서 미분 연산자 를 나타낸다.
를 나타낸다.
| [숨기기] 압축 방식 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 이론 | |||||||||
| 무손실 압축 |
| ||||||||
| 오디오 압축 |
| ||||||||
| 이미지 압축 |
| ||||||||
| 영상 압축 |
| ||||||||
| 압축 형식에서는 형식에 대해서, 데이터 압축 구현에서는 코덱에 대해서 확인하세요. | |||||||||
자료 출처 : https://ko.wikipedia.org/wiki/%ED%95%A9%EC%84%B1%EA%B3%B1
반응형
'개인공간 > 기타' 카테고리의 다른 글
| 2006년 명왕성이 퇴출된 이유 (0) | 2016.08.29 |
|---|---|
| [스크랩] 지킬+깃허브+마크다운=블로그 (0) | 2016.05.07 |
| OAuth 남용은 ID 도용을 일으킬 수 있습니다 (0) | 2015.07.22 |
| 골전도 기능을 갖는 통신단말기 (0) | 2015.03.11 |
| 에테리움 (0) | 2015.03.08 |
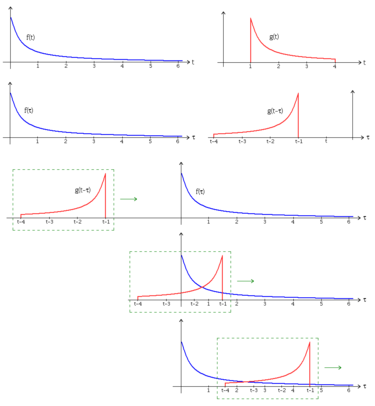
 를 정의함) 이제 정의한 변수를 축으로 두 함수의 파형을 그린다. 그 다음으로 두 함수 중 하나를 선택해
를 정의함) 이제 정의한 변수를 축으로 두 함수의 파형을 그린다. 그 다음으로 두 함수 중 하나를 선택해